1. Riemann Hipotezi:
Matematik dünyasının en ünlü ve en zor sorularından biri olan Riemann Hipotezi, 1859 yılında Alman matematikçi Bernhard Riemann tarafından ortaya atıldı. Hipotez, asal sayıların dağılımını inceleyen bir problem olup, asal sayıların sıklığını belirleyen bir fonksiyon olan Riemann Zeta Fonksiyonu ile ilgilidir. Riemann, bu fonksiyonun tüm non-trivial sıfırlarının, yani sıfırlarının, belirli bir çizgi üzerinde yer alacağını iddia etti. Yani, bu sıfırlar kritik çizgi denen bir çizgide olmalıdır.
Bu hipotez, sayılar teorisi için büyük bir öneme sahiptir ve birçok matematiksel teorinin temelini oluşturur. Ancak 150 yıl sonra bile, bu hipotez hala çözülmemiştir. Çözümünün, asal sayıların dağılımı hakkında önemli bilgiler sunacağı ve matematiksel teoriye ışık tutacağı düşünülüyor.
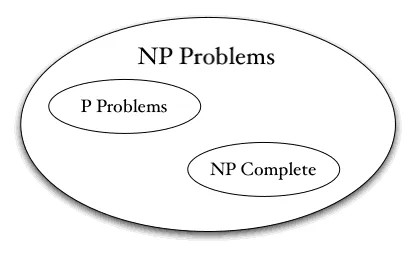
2. P vs NP Problemi:
Bir diğer çözülmemiş matematiksel soru ise P vs NP problemdir. Bu problem, 1971 yılında Stephen Cook tarafından formüle edilmiştir. Problemin özü, bir çözümü doğrulamak kolay olan bir problemin, aynı zamanda kolayca çözülebilir olup olmadığıyla ilgilidir. Yani, P sınıfındaki problemler hızlıca çözülebilen problemleri, NP sınıfındaki problemler ise doğrulaması hızlı fakat çözmesi zor problemleri içerir.
P vs NP problemi, bilgisayar bilimi, algoritmalar ve şifreleme gibi alanlarda devrimsel bir etkiye sahip olabilir. Eğer P = NP olduğu kanıtlanırsa, günümüzün en karmaşık şifreleme teknikleri hızla çözülebilir ve bilgisayar bilimi yeniden şekillenebilir. Ancak bu problem 50 yıldır çözülmemiş ve hala en zor sorulardan biri olarak matematik dünyasında yerini koruyor.
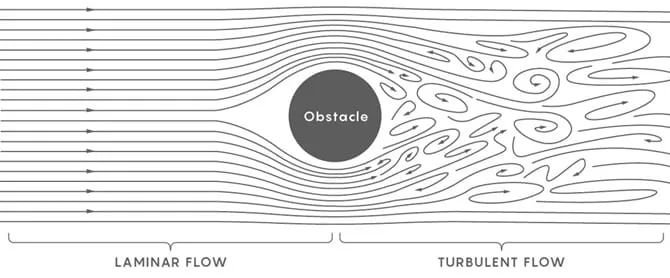
3. Navier-Stokes Denge Denklemleri:
Matematiksel fizik dünyasında önemli bir yere sahip olan Navier-Stokes denklemleri, akışkanların hareketini modelleyen temel denklemlerden biridir. Bu denklemler, sıvıların ve gazların nasıl hareket ettiğini anlamamıza yardımcı olur. Ancak, bu denklemlerin genellikle çözümü oldukça zor ve karmaşıktır. Özellikle üç boyutlu, sıvı akışını modelleyen denklemler, matematiksel olarak çözülemeyen karmaşık yapılar içerir.
Navier-Stokes denklemleri, fiziksel dünyadaki birçok önemli sorunun çözümünde de kullanılır. Örneğin, hava akışlarını modellemek, deniz akıntılarını anlamak ve petrol ve gaz endüstrisindeki akışları çözmek için bu denklemler gereklidir. Ancak, matematikçilerin bu denklemleri çözerken karşılaştıkları en büyük zorluk, çözümdeki tekilliklerdir. Yani, bu denklemlerin bazı durumlar için geçerli çözümleri yoktur.
4. Goldbach Hipotezi:
Goldbach Hipotezi, 1742 yılında Alman matematikçi Christian Goldbach tarafından öne sürüldü. Bu hipotez, her çift sayının, iki asal sayının toplamı olarak ifade edilebileceğini iddia eder. Örneğin, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5 gibi. Ancak, bu iddianın doğruluğu henüz kanıtlanabilmiş değil. Yüzyıllar boyunca birçok matematikçi, hipotezi doğrulamak için büyük çabalar sarf etti, ancak kesin bir çözüm ortaya konamadı.
Goldbach Hipotezi, asal sayılar teorisi ile çok yakından ilişkilidir ve bu sorunun çözülmesi, sayılar teorisine dair yeni bir anlayışa yol açabilir. Günümüz bilgisayarlarıyla yapılan hesaplamalar, hipotezin çok büyük sayılar için doğru olduğunu gösterse de, genel bir kanıt henüz bulunamamıştır.
5. Hodge Hipotezi:
Hodge Hipotezi, geometrinin en zor ve derin sorularından biridir. 1950'lerde matematikçi W.V.D. Hodge tarafından ortaya atılan bu hipotez, algebraik geometri ile ilgilidir ve karmaşık geometrik yapılarla ilgili bir iddiada bulunur. Hodge Hipotezi, karmaşık geometrik şekillerin belirli bir sınıfının, sayılabilir (rasyonel) sınıflarla ilişkilendirilebileceğini öne sürer. Bu hipotez, genellikle Yüksek Matematik alanında, özellikle 10. boyutlu uzaylarla ilgili yapılan çalışmalarla bağlantılıdır.
Ancak, Hodge Hipotezi, karmaşık yapıları anlamak ve bu yapılarla ilgili doğru bir teori geliştirmek açısından oldukça zorlayıcıdır. Bugüne kadar bu hipotez üzerinde birçok çalışma yapılmış olsa da, kesin bir çözüm elde edilememiştir.